In the last lesson we introduced logistic regression as a predictive modeling technique for classification tasks. While logistic regression can serve as a low variance baseline model, other models often yield better predictive performance. Decision trees are another relatively simple classification model that have more expressive power than logistic regression.
Decision Trees in R
If you've ever had to diagnose a problem with an appliance, car or computer, there's a good chance you've encountered a troubleshooting flowchart. A flowchart is a tree-like structure of yes/no questions that guides you through some process based on your specific situation. A decision tree is essentially a flow chart for deciding how to classify an observation: it consists of a series of yes/no or if/else decisions that ultimately assign each observation to a certain probability or class. The series of yes/no decisions can be depicted as a series of branches that lead decisions or "leaves" at the bottom of the tree.
When working with the Titanic survival prediction data last time, we suggested a simple model that classifies all women as survivors and all men as non survivors. This model is an example of a simple decision tree with only one branch or split.
Let's create the gender-based model on the Titanic training set using decision trees in R. First we'll load and preprocess the Titanic data:
In [1]:
library(caret)
In [2]:
setwd("C:/Users/Greg/Desktop/Kaggle/titanic")
titanic_train <- read.csv("titanic_train.csv")
titanic_train$Pclass <- ordered(titanic_train$Pclass, # Convert to ordered factor
levels=c("3","2","1"))
impute <- preProcess(titanic_train[,c(6:8,10)], # Impute missing ages
method=c("knnImpute"))
titanic_train_imp <- predict(impute, titanic_train[,c(6:8,10)])
titanic_train <- cbind(titanic_train[,-c(6:8,10)], titanic_train_imp)
Next, we need to install and load the "rpart" package to use generate decision tree models and the "rpart.plot" package to print nice plots of the trees we generate.
In [3]:
#install.packages("rpart") # Uncomment to install rpart
#install.packages("rpart.plot") # Uncomment to install rpart.plot
library(rpart)
library(rpart.plot)
To create a decision tree, pass a formula of the form response ~ explanatory to the rpart() function:
In [4]:
gender_tree <- rpart(Survived ~ Sex, # Predict survival based on gender
data = titanic_train) # Use the titanic training data
prp(gender_tree ) # Plot the decision tree
*Note: You can have the model show class assignments instead of probabilities by including the method ="class" argument.
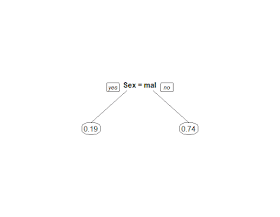
It appears that the rpart() function managed to create our simple gender based model: if a passenger is a male the model gives him a 19% chance of survival while non males have a 74% chance of survival. Let's create a new decision tree that adds the passenger class variable:
In [5]:
class_tree <- rpart(Survived ~ Sex + Pclass, # Predict survival based on gender
data = titanic_train) # Use the titanic training data
prp(class_tree ) # Plot the decision tree
Adding more variables to a decision tree lets it create more branches resulting in a more complex model with greater expressive power. In this case we see that within each gender, the model assigns a lower survival probability to passenger with lower passenger classes: men of class 3 and 2 only have a 14% chance of survival while women of classes 2 and 1 have a 95% chance of survival. It is interesting to note, however, that despite this new layer of branches, the classification predictions this model would output is the same as the original gender based model: all males still have a survival probability below 0.5 and all women have a survival probability of 0.5 or higher.
Let's try adding a few more variables to create a more complex decision tree:
In [6]:
complex_tree <- rpart(Survived ~ Sex + Pclass + Age + SibSp + Fare + Embarked,
cp = 0.001, # Set complexity parameter*
data = titanic_train) # Use the titanic training data
prp(complex_tree) # Plot the decision tree
*Note: the complexity parameter governs model complexity. A smaller complexity parameter will allow for more complex models.
The plot above illustrates how complex decision trees can become when you start adding several explanatory variables. A model that is too complex is prone to overfitting the training data, which can lead to poor generalization to unseen data. The rpart() function includes several optional parameters that you can set to control model complexity. As noted above, the "cp" parameter lets you adjust model complexity (cp adjusts the improvement of the model fit necessary for it to create a new branch.). Apart from the complexity parameter you can also adjust the maximum depth of the tree and the minimum number of observations at each leaf node to limit model complexity:
In [7]:
limited_complexity_tree <- rpart(Survived ~ Sex + Pclass + Age + SibSp +Fare+Embarked,
cp = 0.001, # Set complexity parameter
maxdepth = 5, # Set maximum tree depth
minbucket = 5, # Set min number of obs in leaf nodes
method = "class", # Return classifications instead of probs
data = titanic_train) # Use the titanic training data
prp(limited_complexity_tree) # Plot the decision tree
The model above seems a little more reasonable. Let's use this model to generate predictions on the training set and check the accuracy with a confusion matrix:
In [8]:
train_preds <- predict(limited_complexity_tree,
newdata=titanic_train,
type="class") # Return class predictions
confusionMatrix(train_preds, titanic_train$Survived)
Out[8]:
The tree model has an accuracy of 0.8414 on the training set, but we'd expect it to perform well on the data set used to create it. Let's use the model to make predictions on the Titanic test data and submit them to Kaggle to see how well it performs on unseen data:
In [9]:
titanic_test <- read.csv("titanic_test.csv")
titanic_test$Pclass <- ordered(titanic_test$Pclass, # Convert to ordered factor
levels=c("3","2","1"))
# Impute missing test set ages using the previously constructed imputation model
titanic_test_imp <- predict(impute, titanic_test[,c(5:7,9)])
titanic_test <- cbind(titanic_test[,-c(5:7,9)], titanic_test_imp)
In [10]:
test_preds <- predict(limited_complexity_tree,
newdata=titanic_test,
type="class")
prediction_sub <- data.frame(PassengerId=titanic_test$PassengerId, Survived=test_preds)
write.csv(prediction_sub, "tutorial_dectree_submission.csv", row.names=FALSE)
Upon submission, the this tree-based model gives an accuracy score of 0.77990, which is slightly better than the accuracy we achieved with logistic regression and the simple gender-based model. It turns out that if we had created predictions using the complex tree-based model, we would have achieved an accuracy of 0.75598 on the test data, which is even worse than the simple gender-based model. This underscores the point that complex models are often worse than simpler ones. As Albert Einstein once said, "everything should be as simple as possible, but not simpler." In other words, a model needs to be complex enough to capture patterns in the data, but unnecessary complexity can lead to problems.
Holdout Validation and Cross Validation
When creating a predictive model, we'd like to get an accurate sense of its ability to generalize to unseen data before actually going out and using it on unseen data. As we saw earlier, generating predictions on the training data itself to check the model's accuracy does not work very well: a complex model may fit the training data extremely closely but fail to generalize to new, unseen data. We can get a better sense of a model's expected performance on unseen data by setting a portion of our training data aside when creating a model, and then using that set aside data to evaluate the model's performance. This technique of setting aside some of the training data to assess a model's ability to generalize is known as validation.
Holdout validation and cross validation are two common methods for assessing a model before using it on test data. Holdout validation involves splitting the training data into two parts, a training set and a validation set, building a model with the training set and then assessing performance with the validation set. In theory, model performance on the hold-out validation set should roughly mirror the performance you'd expect to see on unseen test data. In practice, holdout validation is fast and it can work well, especially on large data sets, but it has some pitfalls.
Reserving a portion of the training data for a holdout set means you aren't using all the data at your disposal to build your model in the validation phase. This can lead to suboptimal performance, especially in situations where you don't have much data to work with. In addition, if you use the same holdout validation set to assess too many different models, you may end up finding a model that fits the validation set well due to chance that won't necessarily generalize well to unseen data. Despite these shortcomings, it is worth learning how to use a holdout validation set in R.
You can create a holdout validation set using the createDataPartition() function from the caret package. This function takes a target variable to split upon and a desired split ratio and returns a vector of indexes you can use to split the data into parts where the target variable is distributed evenly between both parts. Let's use createDataPartition() to split the titanic training data into a training and validation set. It is common to put 20 to 30 percent of the data in the validation set and use the rest for training:
In [11]:
set.seed(12)
split_model <- createDataPartition(y=titanic_train$Survived, # Split on survived
list = FALSE, # Return indexes as a vector
p=0.75, # 75% of data in the training set
times=1) # Make 1 split
training_set <- titanic_train[split_model,] # Get the new training set
validation_set <- titanic_train[-split_model,] # Get the validation set
nrow(training_set)/nrow(titanic_train) # Check proportion in each partition
nrow(validation_set)/nrow(titanic_train)
Out[11]:
Out[11]:
The output above shows that we successfully created a new training set with roughly 75% of the original data and a validation set with 25% of the data. We could proceed by building models with this new training set and making predictions on the validation set to assess the models.
Cross validation is a popular alternative to holdout validation that involves splitting the training data into two or more partitions and creating a model for each partition where the partition acts as the validation set and the remaining data acts as the training data. A common form of cross validation is "k-fold" cross validation, which randomly splits data into some number k (a user specified parameter) partitions and then creates k models, each tested against one of the partitions. Each of the k models are then combined into one aggregate final model.
The primary advantage of cross validation is it uses all the training data to build and assess the final model. The main drawback is that building and testing several models can be computationally expensive, so it tends to take much longer than holdout validation.
You can perform cross validation in R using the caret package. The caret package contains a model training function called train() with interfaces to many of R's predictive modeling functions, such as the linear regression model, logistic regression model and decision trees we've seen thus far. You can use this training function with certain control parameters to train models using cross validation. Here's an example of how to perform cross validation with the caret package's model training function:
In [12]:
set.seed(12)
titanic_train$Survived <- as.factor(titanic_train$Survived) # Convert target to factor*
# Create a trainControl object to control how the train function creates the model
train_control <- trainControl(method = "repeatedcv", # Use cross validation
number = 10, # Use 10 partitions
repeats = 2) # Repeat 2 times
# Set required parameters for the model type we are using**
tune_grid = expand.grid(cp=c(0.001))
# Use the train() function to create the model
validated_tree <- train(Survived ~ Sex + Pclass + Age + SibSp + Fare + Embarked,
data=titanic_train, # Data set
method="rpart", # Model type(decision tree)
trControl= train_control, # Model control options
tuneGrid = tune_grid, # Required model parameters
maxdepth = 5, # Additional parameters***
minbucket=5)
validated_tree # View a summary of the model
Out[12]:
*Note: the caret train() function expects the target response variable to be a factor for classification.
**Note: required parameters vary from one model type to another. See a list of model types the caret train function can use and the required parameters here. You can supply a vector of more than one setting for each parameter. If you do so, the train function builds one model for each combination of model parameters and returns uses the best combination for the final model (this method of searching the parameter space by building many models is known as a grid search.).
***Note: Parameters that aren't required by the caret training function but that are accepted by the model type you are using (in this case, rpart for decision trees) may be passed in as additional arguments.
The model summary shows that we trained a CART model (classification and regression tree) with 10-fold cross validation with a validation accuracy of 0.822. You can use a model built using caret's train() function to create predictions using predict() just like we did with lm(), glm() and rpart() models. Since the caret package's train() function offers interfaces to a variety of predictive models along with built-in validation tools, it is one of the most powerful tools at your disposal for predictive modeling in R.
Wrap Up
Decision trees are an easily interpretable yet surprisingly expressive form of predictive model. A decision tree of limited depth can provide a good starting point for classification tasks and model complexity is easy adjustable. For our final lesson, we'll learn about random forests, an extension of decision trees that preform very well on a wide range of classification tasks.
Great blog! Thank you very much for sharing knowledge
ReplyDelete