In the last lesson we introduced linear regression as a predictive modeling method to estimate numeric variables. Now we turn our attention to classification: prediction tasks where the response variable is categorical instead of numeric. In this lesson, we will learn how to use a common classification technique known as logistic regression and apply it to the Titanic survival data we used in lesson 13.
Logistic Regression Basics
Logistic regression is a classification method built on the same concept as linear regression. With linear regression, we take linear combination of explanatory variables plus an intercept term to arrive at a prediction. For example, last time, our simplest linear regression model was:
Linear regression determines which constants minimize the error this linear combination produces on the input data.
In classification problems, the response variable is categorical. The simplest case of classification is where the response variable is binary, meaning it can only take one of two values, such as true or false. Logistic regression takes a linear combination of explanatory variables plus an intercept term just like linear regression, but then it takes the result and passes it through a "logistic" function. The logistic or sigmoid function used for logistic regression is defined as:
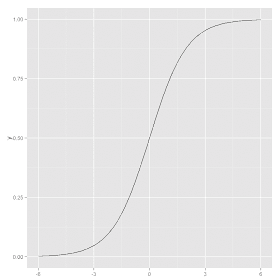
where t is the same linear combination of variables used in linear regression. The sigmoid function looks like an elongated S when plotted:
In [1]:
library(ggplot2)
The sigmoid function is bounded below by 0 and bounded above by 1. In logistic regression, the output is interpreted as a probability: the probability that an observation belongs to the second of the two categories being modeled. When the linear combination of variables produces positive numbers, the resulting probability is greater than 0.5 and when it produces negative numbers, the probability is less than 0.5.
We won't go deeper into the details behind how logistic regression works, but instead focus on how to use it in R. The most important thing to know is that logistic regression outputs probabilities that we can use to classify observations.
Revisiting the Titanic
For the remainder of the lesson we'll be working with the Titanic survival training data from Kaggle that we saw in lesson 13. We'll start by loading the data and then carrying out a few of the same preprocessing tasks we did in lesson 13:
In [3]:
library(caret)
In [4]:
setwd("C:/Users/Greg/Desktop/Kaggle/titanic")
titanic_train <- read.csv("titanic_train.csv")
titanic_train$PassengerId <- NULL # Remove PassengerId
titanic_train$Ticket <- NULL # Remove Ticket
titanic_train$Name <- as.character(titanic_train$Name) # Convert name to character
titanic_train$Pclass <- ordered(titanic_train$Pclass, # Convert to ordered factor
levels=c("3","2","1"))
# Reduce cabin factor levels
char_cabin <- as.character(titanic_train$Cabin)
new_Cabin <- ifelse(char_cabin == "",
"",
substr(char_cabin,1,1))
new_Cabin <- factor(new_Cabin )
titanic_train$Cabin <- new_Cabin
In [5]:
impute <- preProcess(titanic_train[,c(5:8)], # Impute missing ages*
method=c("knnImpute"))
titanic_train_imp <- predict(impute, titanic_train[,c(5:8)])
titanic_train <- cbind(titanic_train[,c(1:4)], titanic_train_imp, titanic_train[,c(9:10)])
In [6]:
summary(titanic_train)
Out[6]:
*Note: we use only use the numeric variables, Age, sibSp, Parch and Fare for imputation because the impute function we learned only accepts numeric variables. If we wanted more accurate imputation, we could convert categorical variables like Sex and Pclass into several numeric 0,1 numeric indicator variables (dummy variables.). Converting a factor into 0,1 dummy variables is known as one-hot encoding. Also note that the preProcess() function scales and centers the data before imputation.
Now we are ready to use a logistic regression model to predict survival. You can make a logistic regression model by passing a formula to the glm() function. Let's make a logistic regression model that only uses the Sex variable as a predictor:
In [7]:
titanic_model <- glm(Survived ~ Sex, # Formula
data= titanic_train, # Data set
family="binomial") # family="binomial" for binary logistic
summary(titanic_model) # Check model summary
Out[7]:
The summary output for the logistic regression model coefficients looks similar to the output we saw for linear regression. We can see the model produced a positive intercept value and a weight of -2.5051 placed on gender level of male and that both the intercept and male variables have high significance. Note that the first level of each class you pass into the model is treated as the default, so we don't need a separate variable for female. Let's use the model to make predictions on the test set:
In [8]:
train_preds <- predict(titanic_model, # Model to use
newdata=titanic_train, # Data to use for predictions
type="response") # Return predicted probabilities
table(train_preds, titanic_train$Sex)
Out[8]:
The table shows that the model predicted a survival chance of roughly 19% for males and 74% for females. If we used this simple model to predict survival, we'd end up predicting that all women survived and that all men died. Let's make a more complicated model that includes a few more variables from the titanic training set:
In [9]:
titanic_model <- glm(Survived ~ Sex+Pclass+Age+SibSp+Cabin,
data= titanic_train,
family="binomial")
predicted_probabilities <- predict(titanic_model,
newdata=titanic_train,
type="response")
summary(titanic_model)
Out[9]:
We can convert the predicted probabilities to class predictions by assuming that any observation with a predicted probability of 0.5 or above is a positive result (in this case, survived) and that cases below 0.5 are negative for the class we are predicting:
In [10]:
class_preds <- ifelse(predicted_probabilities >= 0.5, 1, 0) # Convert to 0, 1 preds
result_table <- table(class_preds, # Make a table of predictions vs. actual
titanic_train$Survived)
result_table
Out[10]:
The table above shows the classes our model predicted vs. true values of the Survived variable. This table of predicted vs. actual values is known as a confusion matrix.
The Confusion Matrix
The confusion matrix is a common tool for assessing the results of classification. Each cell tells us something different about our predictions versus the true values. The bottom right corner indicates the True positives: people the model predicted to survive who actually did survive. The bottom left cell indicates the false positives: people for whom the model predicted survival who did not actually survive. The top left cell indicates the true negatives: people correctly identified as non survivors. Finally the top right cell shows the false negatives: passengers the model identified as non survivors who actually did survive.
We can calculate the overall prediction accuracy from the matrix by adding the total number of correct predictions and dividing by the total number of predictions. In the case of our model, the prediction accuracy is:
In [11]:
(472+238)/sum(result_table)
Out[11]:
Overall prediction accuracy is just one of many quantities you can use to assess a classification model. Oftentimes accuracy is not the best metric for assessing a model.
Consider a model made to predict the occurrence of a disease that only occurs in 0.01% of people. A model that never predicts that anyone has the disease would be 99.99% accurate, but it also wouldn't help save lives. In this case, we might be more interested in the model's sensitivity: the proportion of positive cases that the model correctly identifies as positive.
Relying only on sensitivity can also be a problem. Consider a new model that predicts everyone has the disease. This new model would achieve a sensitivity score of 100% since it would correctly label everyone who has the disease as having the disease. In this case, the model's specificity--the number negative cases the model correctly identifies as negative--is zero, so the model loses any value for distinguishing between the classes.
We won't discuss all the different evaluation metrics that fall out the confusion matrix, but it is a good idea to consider accuracy as well as sensitivity and specificity when assessing model performance. We can view these metrics as well as several others using the caret package's confusionMatrix() function. Let's run it on our Titanic predictions:
In [12]:
confusionMatrix(data= class_preds,
reference= titanic_train$Survived,
positive = "1") # Set the positive class to Survived
Out[12]:
The confusion matrix summary output confirms our accuracy calculation and shows us several other evaluation metrics. Balanced accuracy is the average of sensitivity and specificity, which can give us a better sense of overall model performance than pure accuracy.
For the Titanic competition, accuracy is the scoring metric used to judge the competition, so we don't have to worry too much about other metrics.
As a final exercise, let's use our logistic regression model to make predictions for the Titanic test set. First we need to load and prepare the test data using the same steps we used to prepare the training data:
In [13]:
titanic_test <- read.csv("titanic_test.csv")
ids <- titanic_test$PassengerId
titanic_test$PassengerId <- NULL
titanic_test$Ticket <- NULL
titanic_test$Name <- as.character(titanic_test$Name)
titanic_test$Pclass <- ordered(titanic_test$Pclass,
levels=c("3","2","1"))
char_cabin <- as.character(titanic_test$Cabin)
new_Cabin <- ifelse(char_cabin == "",
"",
substr(char_cabin,1,1))
new_Cabin <- factor(new_Cabin )
titanic_test$Cabin <- new_Cabin
In [14]:
# Impute missing test set ages using the previously constructed imputation model
titanic_test_imp <- predict(impute, titanic_test[,c(4:7)])
titanic_test <- cbind(titanic_test[,c(1:3)], titanic_test_imp, titanic_test[,c(8:9)])
summary(titanic_test) # check test data
Out[14]:
Now we can use our model to make predictions and save the result to a file:
In [15]:
test_preds <- predict(titanic_model,
newdata=titanic_test,
type="response")
class_preds <- ifelse(test_preds >= 0.5, 1, 0)
prediction_sub <- data.frame(PassengerId=ids, Survived=class_preds)
write.csv(prediction_sub, "tutorial_logreg_submission.csv", row.names=FALSE)
It turns out that upon submission, this logistic regression model has an accuracy score of 0.76555, which is the exact same accuracy score as the simplistic women survive, men die model. It could be that the gender variable is dominating our model so powerfully that it always predicts men die and women survive. We can investigate this with a table:
In [16]:
table(titanic_test$Sex, class_preds)
Out[16]:
The model actually does predict that a few men survived and that a few women died, but it still makes no improvement over the basic gender-based model.
Wrap Up
Logistic regression is a common tool for generating class probabilities and predictions. Although logistic regression models are simple and often insufficient to fully capture relationships between variables in many predictive modeling tasks, they are a good starting point because simple models tend not to overfit the data. Next time we will explore another predictive modeling technique for classification: decision trees.
No comments:
Post a Comment
Note: Only a member of this blog may post a comment.